In this post I will show how to combine features from natural language processing with traditional features (meta data) in one single model in keras (end-to-end learning). The solution is a multiple inputs model.
Problem definition
Scientific data sets are usually limited to one single kind of data, for example text, images or numerical data. This makes a lot of sense, as the goal is to compare new with existing models and approaches. Anyway, often ml models combine more then one single data source and therefore deal with different kinds of data. To utilize end-to-end learning neural networks, instead of manually stacking models, we need to combine these different feature spaces inside the neural network.
Let´s assume we want to solve a text classification problem and we do have additional meta data for each of the documents in our corpus. In simple approaches, where our document is represented by a bag of words, we could just add our metadata to the BoW vector, and we are done. But when using word embeddings it´s a bit more complicated.
Special Embeddings
The easiest solution is to add our meta data as additional special embeddings. In this case we need to transform our data into categorial features, because our embeddings can exist or not exist. This works if we increase the vocabulary size by the number of additional features and treat them as additional words.
Example: Our dictionary is 100 words and we have 10 additional features. In this case we add 10 additional words to the dictionary. The sequence of embeddings now always starts with the meta data features, therefore we must increase our sequence length by 10. Each of these 10 special embeddings represent one of the added features.
There are several drawbacks with this solution. We only have categorical features, not continuous values and even more important our embedding space mixes up nlp and meta data.
Multiple input models
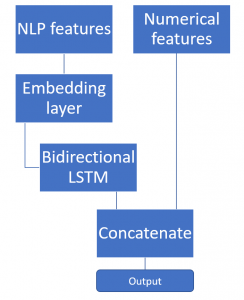
Much better is a model, which can handle continuous data and just works as a classifier with nlp features and meta data. This is possible with multiple inputs in keras. Example:
nlp_input = Input(shape=(seq_length,), name='nlp_input') meta_input = Input(shape=(10,), name='meta_input') emb = Embedding(output_dim=embedding_size, input_dim=100, input_length=seq_length)(nlp_input) nlp_out = Bidirectional(LSTM(128, dropout=0.3, recurrent_dropout=0.3, kernel_regularizer=regularizers.l2(0.01)))(emb) x = concatenate([nlp_out, meta_input]) x = Dense(classifier_neurons, activation='relu')(x) x = Dense(1, activation='sigmoid')(x) model = Model(inputs=[nlp_input , meta_input], outputs=[x])
We use a bidirectional LSTM model and combine its output with the metadata. Therefore we define two input layers and treat them in separate models (nlp_input and meta_input). Our NLP data goes through the embedding transformation and the LSTM layer. The meta data is just used as it is, so we can just concatenate it with the lstm output (nlp_out). This combined vector is now classified in a dense layer and finally sigmoid in to the output neuron.
This concept is usable for any other domain, where sequence data from RNNs is mixed up with non-sequence data. The output of an LSTM is representing the Sequence in an intermidiate space. That means the output of the LSTM is also a special kind of embedding.


[…] is even possible to add meta data (numerical) to the model, as described in the previous post.In this metadata the information about the author of each message can be stored and furthermore […]
So let’s say I made this model and I only have text to classify and not the numerical features, will the model predict correctly?
If you were to add another LSTM layer or another NN layer, how would you need to modify the code above?
Hi Christopher,
if you want to stack the LSTM layer, you can this:
Hi,
Awesome post! I was wondering how we can use an LSTM to perform text classification using numeric data. For example, suppose I have a dataframe with 11 columns and 100 rows, and columns 1-10 are the features (all numeric) while column 11 has sentences (targets). I gave a thought over the multiple input model which is described in this post which is quite useful when the features are a mix of numeric and text, but in this case, it would be like using the numeric features to predict the sentences. Any minimal example regarding this is highly appreciated.
What do you mean excatly, you want to predict the sentences in terms of generating sentences or just using the sentence as class?
Hi. I would like to predict the sentences based on the numeric features. So it would be something like using these numeric features and the model would have sentences as targets instead of just an integer label. I can make it more precise with some code I am trying, but am not sure why I am always getting the same sentences as output. I would make this more clear, I have a data frame with many rows and columns (dimensions 21392×1973). I would like to use columns from 1-1972 (which are all numeric) as features, while column 1973 (the last column in dataframe has sentences within). So basically, by providing the model with new features from a test set, I want to predict the sentences. I am trying this approach but feel that I am doing something wrong, especially with a major confusion in choosing the loss and activation (as I’ve one hot encoded sentences in the last column and am inverse transforming them back in the end). Any suggestions and guidance would be highly appreciated. I regularly read your blogs, and am looking for an approach for data-text based LSTM:-)
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from keras.models import load_model
df = pd.read_pickle(‘my_data.pkl’) # Here, I am reading the data which is completely structured
df_features = df.iloc[:,:-1] # These are the numeric features as inputs
outputs_df = df.iloc[:,-1] # These are outputs (all sentences)
outputs_df = outputs_df.values # Converting the outputs to an array
# center and scale to ensure numeric features have values between 0-1 (as all have different ranges)
print(“Center and Scaling taking place….”)
scaler = MinMaxScaler(feature_range=(0, 1))
df_features = scaler.fit_transform(df_features)
# # one-hot encode the outputs (which are the sentences)
print(“One hot encoding the outputs for training….”)
onehot_encoder = OneHotEncoder()
encode_categorical = outputs_df.reshape(len((outputs_df)), 1)
outputs_encoded = onehot_encoder.fit_transform(encode_categorical).toarray()
print(‘outputs_encoded.shape after One Hot Encode:’, outputs_encoded.shape)
X_train, X_test, y_train, y_test = train_test_split(df_features,outputs_encoded,test_size=0.30) #Splitting data into train and test set
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import TimeDistributed
n_timesteps = len(X_train) #No. of time steps for training data
n_timesteps_test = len(X_test) #No. of time steps for test data
X_train = X_train.reshape(1,n_timesteps,1972)
y_train = y_train.reshape(1,n_timesteps,26)
X_test = X_test.reshape(1,n_timesteps_test,1972)
y_test = y_test.reshape(1,n_timesteps_test,26)
# create a sequence classification instance
def get_sequence(n_timesteps, X, y):
X = X.reshape(1, n_timesteps, 1972)
y = y.reshape(1, n_timesteps, 26)
return X, y
# define LSTM
model_lstm = Sequential()
model_lstm.add(LSTM(100, input_shape=(None, 1972), return_sequences=True))
model_lstm.add(TimeDistributed(Dense(26, activation=’sigmoid’)))
model_lstm.compile(loss=’binary_crossentropy’, optimizer=’adam’, metrics=[‘acc’])
# fitting model
X, y = get_sequence(n_timesteps, X_train, y_train)
# training LSTM
model_lstm.fit(X, y, epochs=100, batch_size=128, verbose=2)
# evaluate LSTM on test data
yhat_lstm_test = model_lstm.predict(X_test, verbose=0)
yhat_squeezed_lstm_test = np.squeeze(yhat_lstm_test, axis=0)
yhat_sentences_lstm_test = onehot_encoder.inverse_transform(yhat_squeezed_lstm_test) # These are the sentences, but weirdly all are generated as same, which is not the case in the y_test (original test sentences)
So basically, I would like to predict sentences in the sense of language generation with the LSTM. Thanks.
It would go beyond the scope here to go through in detail, sorry. Mabye I come back to your example later on.
Basically, I would say that the data representation does not meet your requirements. Your label is a bag of words vector with 26 words * n_timesteps. And you are trying to predict a new bag of words vector for each timestep, but your LSTM predicts the first BoW vector after seeing the first timestep in the input sequence (return_sequences). I guess this is not what you want, you need some internal representation of the whole sequence first (sequence embedding).
I would rather use word embeddings, instead of OneHot encoding and a sequence to sequence model (Encoder/Decoder). Maybe this post helps a bit.
Thanks for your reply again. I would really appreciate a blog article on something similar with my example scenario, as it will be very helpful for me and other people looking for something like this. I got your idea of using word embeddings for the outputs, instead of binary one hot encoding and a Seq2Seq model, and a coherent blog article would be much appreciated! Cheers.
[…] Here is a link, where it more detailed. […]
I am new with this, to this might be a really silly question, but I can’t figure out how to shape an input to the requirement shape=(10,). Could you provide a quick example on how to construct this? I have columnar data in a data frame and can convert to np arrays, but I can’t seem to figure out how to store it in the correct shape.
Thanks!
Hi Michael, it’s not a silly question. Assuming you already have the NLP data in the correct format and you additional meta data is a vector of size 10:
Calling the fit method:
where the input for the meta data is a array of samples * number of additional features. e.g.
Quite a nice post of what I was working one, one thing Christopher can we pass the concatenated vector to another LSTM? I understand that LSTM requires a sequential data and numerical data is not sequential in most cases, but I am just bouncing the idea, would it be possible to pass the combined vector to another LSTM.?
You can interpret the concatenated vector as a sequence, but what problem does it solve? As long as you don’t have sequential data, it’s not neccecary to introduce additional complexity. LSTMs are quite complex and in the last years 1D convolutions outperformed LSTMs in many tasks, so I don’t think it helps.
Hi, thank you very much for providing your code. It is very helpful for me to develop my own version of NLP+Metadata classification task. Could you please share with us the shapes of your layers and also of the data? When I am concatenating I am getting this error “ValueError: A `Concatenate` layer requires inputs with matching shapes except for the concat axis. Got inputs shapes: [(None, 500, 128), (None, 500, 1)]”.
I am using an embedding of size 50 with maximum sequence number 500, and I have one additional feature. I transform this feature into one hot encoding with size of 500 (keeping the 500 most popular values of this feature). When I concatenate on axis 1, I get the above error. Concatenating on axis=2 works, but I am not sure whether it is semantically correct. Could you please share more info about your concatenation? Maybe with `model.summary()`? Thanks!
By the way, this is my question in Stackoverflow: https://stackoverflow.com/questions/57592430/keras-functional-api-invalidargumenterror-input-1-should-contain-3-elements-b
I would appreciate it very much if you can have a look and give me answer 🙂
Dear Konstantina, I hope you found a solution. I have this post, where I have some more details, but my seq_len was 250 I think and my embedding space was about 128. I think my metadata vector was 12 or so. I don’t have a summary for you right now, sorry. If you got it working, I suggest to use Conv1D approach, instead of LSTMs. In my case that more robust with the save accuracy. Cheers Christian
Hi, this is exactly what I am trying to do. I am predicting a hotel accomodation type(hotel or apartment) based on the hotel description and other features like hotel amenities(categorical numbers). I understood that I need to pass categorical numbers as the metadata input. I am not sure how I can do in the sequential api. My model is as below:
model = Sequential()
model.add(Conv1D(32, kernel_size=3, activation=’elu’, padding=’same’,input_shape=(vector_size, 1)))
model.add(Conv1D(32, kernel_size=3, activation=’elu’, padding=’same’))
model.add(Conv1D(32, kernel_size=3, activation=’relu’, padding=’same’))
model.add(MaxPooling1D(pool_size=3))
model.add(Bidirectional(LSTM(512, dropout=0.2, recurrent_dropout=0.3)))
model.add(Dense(512, activation=’sigmoid’))
model.add(Dropout(0.2))
model.add(Dense(512, activation=’sigmoid’))
model.add(Dropout(0.25))
model.add(Dense(512, activation=’sigmoid’))
model.add(Dropout(0.25))
model.add(Dense(2, activation=’softmax’))
model.compile(loss=’categorical_crossentropy’, optimizer=Adam(lr=0.0001, decay=1e-6), metrics=[‘accuracy’])
tensorboard = TensorBoard(log_dir=’logs/’, histogram_freq=0, write_graph=True, write_images=True)
model.summary()
So how and where exactly I can add the meta data.
Thanks for the support.
Hi Hemanth, use the functional API. The problem with the sequential API is that you can not have multiple inputs and furthermore the “parallel” conv1D layers are not really parallel. The idea is to have one path which handels the NLP data and one for the rest. To make it working I suggest to remove the Conv1D layers and make it working with the simple LSTMs and later you can replace the LSTM with 1D-convolutions. The key part is: model = Model(inputs=[nlp_input , meta_input], outputs=[x])
Hi,
My data frame “df” is as below:
Hotel_Name Description type label
Radisson Blu Set in a prime location of Waldbronn 47 0
So here I am trying to use “Description” and “type” to do the classification. “label” is the output label.
the description embedding is of shape : (512,1)
meta_input as you can see is a number
I tried as following:
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
from keras.layers.merge import concatenate
# first input model
nlp_out = Bidirectional(LSTM(128, dropout=0.3, recurrent_dropout=0.3, kernel_regularizer=regularizers.l2(0.01)))(embd)
x = concatenate([nlp_out, data_meta])
x = Dense(classifier_neurons, activation=’relu’)(x)
x = Dense(1, activation=’sigmoid’)(x)
model = Model(inputs=[nlp_input , meta_input], outputs=[x])
# summarize layers
print(model.summary())
But this is not working. So how can I reshape my both inputs? Sorry for asking such basic question, I never worked with funcitonal API.
Thanks
What’s your error message and what shapes do your inputs have?
Really interesting. Do you have a dataset for this combining numerical and text features model. I was recently studying deep learning and RNN, I would appreciate if you can give me an access to your dataset for this problem.
Hi James, I don’t have a data set, which I can share, sorry. You might want to take a look at other public data sets here. Cheers
Hi,
Thank you for the wonderful post. Could you please describe what is “Classifier_neuron” in your code above
Hi Anupam, classifier_neurons is just ment as the number of neurons you want to use for the last layer (head), so it depends on your task, but 64 is a good starter.
Hi sir, i found your site are really wonderfull and seems like im running same issue when i try to combine embedding layer which i use text and numerical feature (like sentence length or number of exclamation mark etc)
when i try your code i got error like
A `Concatenate` layer requires inputs with matching shapes except for the concat axis. Got inputs shapes: [(None, 150, 300), (None, 1)]
my text layer consist of 150 len of text and the 300 was the embed size
and my numeric feature is just 1 shape of element (i try number of data length)
this is my snapped code
inp = Input(shape=(maxlen,))
length_input = Input(shape=(1,))
x = Embedding(max_features, embed_size, weights=[embedding_matrix], trainable=False)(inp)
x = concatenate([x, length_input]) <—- i got error in this row
A `Concatenate` layer requires inputs with matching shapes except for the concat axis. Got inputs shapes: [(None, 150, 300), (None, 1)]
x = Bidirectional(CuDNNLSTM(128, return_sequences=True))(x)
x = Bidirectional(CuDNNLSTM(64, return_sequences=True))(x)
so on….
im tryin to move the concatenate code after bidirectional layer and i got same issue
any idea sir ?
thankyou very much
sorry for dumb question :)) have a nice day
Hi Hendri, so you want to concatenate x and length_input, where x is the output of the embedding layer and length_input the vector you want to stack on top the embedding. The output of the embedding layer is a sequence of (word) embeddings. You can’t just concatenate a sequence and your length_input in case it is one dimensional. I guess what you want it to first get the sequence representation of this sequence of words and then stack with that. You can try to move your concatenate layer after your last LSTM (without return_sequences=True). If your length_input is also a sequence you might use concatenate with the axis parameter to concatenate along the sequence. I hope that helps, Cheers
Thanks for the article. Well put together. I do have a question. How do I set up the data set. Do I have to repeat the numerical features in the input data set, one per “word” in the NLP data? Do you have examples of dataset prep for such a network? Thanks again.
Hi Grass, no you don’t have to repeat the numerical feature for every word. The idea is to have two input tensors, where one is the NLP tensor, using word indices and one is the tensor with numerical data. The embedding layer takes the word indices from the nlp_tensor and translates them into a sequence of embeddings, while the numerical tensor only has one vector for every word indices vector. One document, one numerical data.
[…] Ce message a été initialement publié sur mon blog ici. […]
Thanks for the article! I am trying to plan out the best way to create unsupervised clusters on a mix of text and categorical data so there are some awesome parallels I took from your article even though it is classification with lstm. When you mention special embeddings based on one hot encoding, why would we add the one hot encoded 1 or 0 to the embeddings instead of the category word or phrase itself? I guess im asking why One hot encode when you can just append the columns together and add the categorical features as special word embeddings (to guarantee their importance) instead of multiple categories of binary that whatever ml algorithm you use might mix up?
Hi Tyler, sorry for that late reply, I was not checking for comments a long time. I think you can do it that way. My approach was to strictly seperate word embeddings and numerical features, so that the additional information is not mixed in into the text features. However, I think today I would go for a different approach and try to have one embedding for the text and one embedding for all of the numerical features (kind of a numerical feature embedding). Cheers Christian
Hi Christian. Thanks for sharing. I’d like to apply this approach but by using pyspark. Would you by any chance aware that it has been done using pyspark? Thanks.
Hi KC, sorry for that late reply, I was not checking for comments. Not sure how that fit’s into pyspark, you would still need to use any kind of tensorflow model right?. Cheers Christian